[Kaggle] House Prices: Advanced Regression Techniques

Posted on In Symbols count in article: 21k Reading time ≈ 19 mins.

房价预测是我入门Kaggle的第二个比赛，参考学习了他人的一篇优秀教程：https://www.kaggle.com/serigne/stacked-regressions-top-4-on-leaderboard

通过Serigne的这篇notebook，我学习到了关于数据分析、特征工程、集成学习等等很多有用的知识，在这里感谢一下这位大佬。

本篇文章立足于Serigne的教程，将他的大部分代码实现了一遍，修正了个别小错误，也加入了自己的一些视角和思考，做了一些自认为reasonable的“改进”。最终在Leaderboard上的得分为0.11676，排名前13%。虽然最后结果反而变差了一点（没有道理啊！QAQ），但我觉得整个实践的过程仍然值得记录一下。

废话不多说，下面进入正文。

数据集概览

导入相关Python包：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#import some necessary librairies

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
%matplotlib inline
import matplotlib.pyplot as plt  # Matlab-style plotting
import seaborn as sns
color = sns.color_palette()
sns.set_style('darkgrid')
import warnings
def ignore_warn(*args, **kwargs):
    pass
warnings.warn = ignore_warn #ignore annoying warning (from sklearn and seaborn)

from scipy import stats
from scipy.stats import norm, skew #for some statistics

pd.set_option('display.float_format', lambda x: '{:.3f}'.format(x)) #Limiting floats output to 3 decimal points

from subprocess import check_output
print(check_output(["ls", "../input"]).decode("utf8")) #check the files available in the directory

sample_submission.csv test.csv train.csv

读取csv文件：

1
2
train = pd.read_csv('datasets/train.csv')
test = pd.read_csv('datasets/test.csv')

查看训练、测试集的大小：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#check the numbers of samples and features
print("The train data size before dropping Id feature is : {} ".format(train.shape))
print("The test data size before dropping Id feature is : {} ".format(test.shape))

#Save the 'Id' column
train_ID = train['Id']
test_ID = test['Id']

#Now drop the  'Id' colum since it's unnecessary for  the prediction process.
train.drop("Id", axis = 1, inplace = True)
test.drop("Id", axis = 1, inplace = True)

#check again the data size after dropping the 'Id' variable
print("\nThe train data size after dropping Id feature is : {} ".format(train.shape)) 
print("The test data size after dropping Id feature is : {} ".format(test.shape))

The train data size before dropping Id feature is : (1460, 81) The test data size before dropping Id feature is : (1459, 80)

The train data size after dropping Id feature is : (1460, 80) The test data size after dropping Id feature is : (1459, 79)

特征工程

离群值处理

通过绘制散点图可以直观地看出特征是否有离群值，这里以GrLivArea为例。

1
2
3
4
5
fig, ax = plt.subplots()
ax.scatter(x = train['GrLivArea'], y = train['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()
img

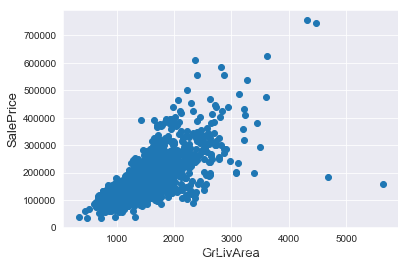
我们可以看到图像右下角的两个点有着很大的GrLivArea，但相应的SalePrice却异常地低，我们有理由相信它们是离群值，要将其剔除。

1
2
3
4
5
6
7
8
9
#Deleting outliers
train = train.drop(train[(train['GrLivArea']>4000) & (train['SalePrice']<300000)].index)

#Check the graphic again
fig, ax = plt.subplots()
ax.scatter(train['GrLivArea'], train['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()
img

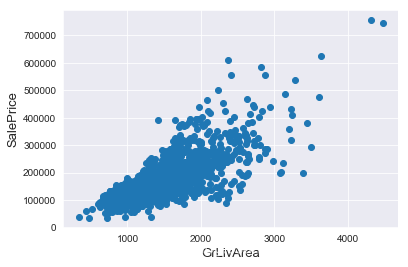
值得一提的是，删除离群值并不总是安全的。我们不能也不必将所有的离群值全部剔除，因为测试集中依然会有一些离群值。用带有一定噪声的数据训练出的模型会具有更高的鲁棒性，从而在测试集中表现得更好。

目标值分析

SalePrice是我们将要预测的目标，有必要对其进行分析和处理。

我们画出SalePrice的分布图和QQ图（Quantile Quantile Plot）。这里简单说一下QQ图，它是由标准正态分布的分位数为横坐标，样本值为纵坐标的散点图。如果QQ图上的点在一条直线附近，则说明数据近似于正态分布，且该直线的斜率为标准差，截距为均值。对于QQ图的详细介绍可以参考这篇文章：https://blog.csdn.net/hzwwpgmwy/article/details/79178485

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
sns.distplot(train['SalePrice'] , fit=norm);

# Get the fitted parameters used by the function
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

#Now plot the distribution
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

#Get also the QQ-plot
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()

mu = 180932.92 and sigma = 79467.79

imgimg

SalePrice的分布呈正偏态，而线性回归模型要求因变量服从正态分布。我们对其做对数变换，让数据接近正态分布。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#We use the numpy fuction log1p which  applies log(1+x) to all elements of the column
train["SalePrice"] = np.log1p(train["SalePrice"])

#Check the new distribution 
sns.distplot(train['SalePrice'] , fit=norm);

# Get the fitted parameters used by the function
(mu, sigma) = norm.fit(train['SalePrice'])
print( '\n mu = {:.2f} and sigma = {:.2f}\n'.format(mu, sigma))

#Now plot the distribution
plt.legend(['Normal dist. ($\mu=$ {:.2f} and $\sigma=$ {:.2f} )'.format(mu, sigma)],
            loc='best')
plt.ylabel('Frequency')
plt.title('SalePrice distribution')

#Get also the QQ-plot
fig = plt.figure()
res = stats.probplot(train['SalePrice'], plot=plt)
plt.show()

mu = 12.02 and sigma = 0.40

imgimg

正态分布的数据有很多好的性质，使得后续的模型训练有更好的效果。另一方面，由于这次比赛最终是对预测值的对数的误差进行评估，所以我们在本地测试的时候也应该用同样的标准。

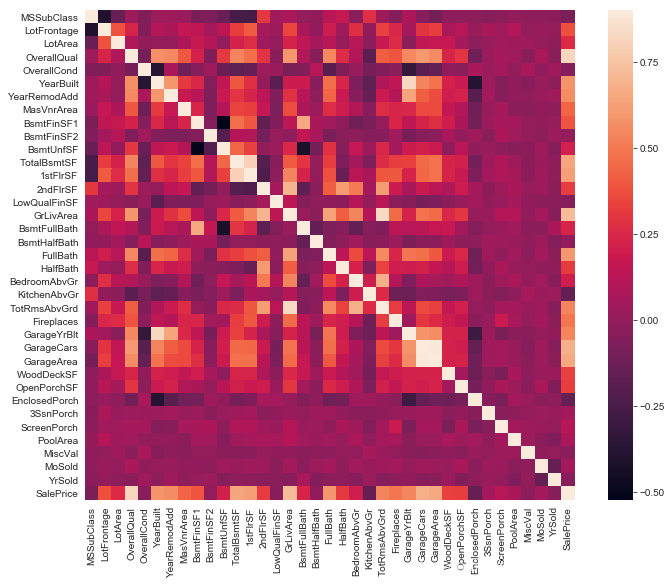
特征相关性

用相关性矩阵热图表现特征与目标值之间以及两两特征之间的相关程度，对特征的处理有指导意义。

1
2
3
4
#Correlation map to see how features are correlated with SalePrice
corrmat = train.corr()
plt.subplots(figsize=(12,9))
sns.heatmap(corrmat, vmax=0.9, square=True)
img

缺失值处理

首先将训练集和测试集合并在一起：

1
2
3
4
5
6
ntrain = train.shape[0]
ntest = test.shape[0]
y_train = train.SalePrice.values
all_data = pd.concat((train, test)).reset_index(drop=True)
all_data.drop(['SalePrice'], axis=1, inplace=True)
print("all_data size is : {}".format(all_data.shape))

all_data size is : (2917, 79)

统计各个特征的缺失情况：

1
2
3
4
all_data_na = (all_data.isnull().sum() / len(all_data)) * 100
all_data_na = all_data_na.drop(all_data_na[all_data_na == 0].index).sort_values(ascending=False)[:30]
missing_data = pd.DataFrame({'Missing Ratio' :all_data_na})
missing_data.head(20)
Missing Ratio
PoolQC 99.691
MiscFeature 96.400
Alley 93.212
Fence 80.425
FireplaceQu 48.680
LotFrontage 16.661
GarageQual 5.451
GarageCond 5.451
GarageFinish 5.451
GarageYrBlt 5.451
GarageType 5.382
BsmtExposure 2.811
BsmtCond 2.811
BsmtQual 2.777
BsmtFinType2 2.743
BsmtFinType1 2.708
MasVnrType 0.823
MasVnrArea 0.788
MSZoning 0.137
BsmtFullBath 0.069 
1
2
3
4
5
6
f, ax = plt.subplots(figsize=(15, 12))
plt.xticks(rotation='90')
sns.barplot(x=all_data_na.index, y=all_data_na)
plt.xlabel('Features', fontsize=15)
plt.ylabel('Percent of missing values', fontsize=15)
plt.title('Percent missing data by feature', fontsize=15)
img

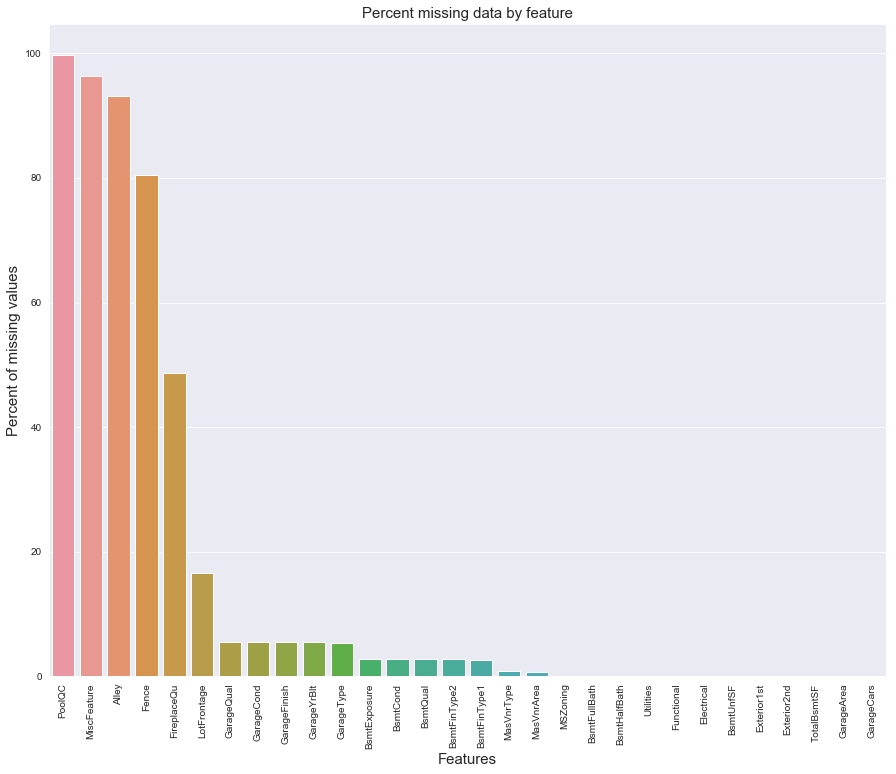
在data_description.txt中已有说明，一部分特征值的缺失是因为这些房子根本没有该项特征，对于这种情况我们统一用“None”或者“0”来填充。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
all_data["PoolQC"] = all_data["PoolQC"].fillna("None")
all_data["MiscFeature"] = all_data["MiscFeature"].fillna("None")
all_data["Alley"] = all_data["Alley"].fillna("None")
all_data["Fence"] = all_data["Fence"].fillna("None")
all_data["FireplaceQu"] = all_data["FireplaceQu"].fillna("None")
all_data["MasVnrType"] = all_data["MasVnrType"].fillna("None")
all_data["MasVnrArea"] = all_data["MasVnrArea"].fillna(0)
for col in ('GarageType', 'GarageFinish', 'GarageQual', 'GarageCond'):
    all_data[col] = all_data[col].fillna('None')
for col in ('GarageYrBlt', 'GarageArea', 'GarageCars'):
    all_data[col] = all_data[col].fillna(0)
for col in ('BsmtFinSF1', 'BsmtFinSF2', 'BsmtUnfSF','TotalBsmtSF', 'BsmtFullBath', 'BsmtHalfBath'):
    all_data[col] = all_data[col].fillna(0)
for col in ('BsmtQual', 'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2'):
    all_data[col] = all_data[col].fillna('None')

对于缺失较少的离散型特征，可以用众数填补缺失值。

1
2
3
4
5
6
all_data['MSZoning'] = all_data['MSZoning'].fillna(all_data['MSZoning'].mode()[0])
all_data['Electrical'] = all_data['Electrical'].fillna(all_data['Electrical'].mode()[0])
all_data['KitchenQual'] = all_data['KitchenQual'].fillna(all_data['KitchenQual'].mode()[0])
all_data['Exterior1st'] = all_data['Exterior1st'].fillna(all_data['Exterior1st'].mode()[0])
all_data['Exterior2nd'] = all_data['Exterior2nd'].fillna(all_data['Exterior2nd'].mode()[0])
all_data['SaleType'] = all_data['SaleType'].fillna(all_data['SaleType'].mode()[0])

对于LotFrontage项，由于每个Neighborhood的房子的LotFrontage很可能是比较相近的，所以我们可以用各个房子所在Neighborhood的LotFrontage的中位数作为填充值。

1
2
3
#Group by neighborhood and fill in missing value by the median LotFrontage of all the neighborhood
all_data["LotFrontage"] = all_data.groupby("Neighborhood")["LotFrontage"].transform(
    lambda x: x.fillna(x.median()))

data_description.txt中还提到过，Functional默认是“Typ”。

1
all_data["Functional"] = all_data["Functional"].fillna("Typ")

Utilities特征有两个缺失值，且只有一个样本是“NoSeWa”，除此之外全部都是“AllPub”，因此该项特征的方差非常小，我们可以直接将其删去。

1
all_data = all_data.drop(['Utilities'], axis=1)

最后确认缺失值是否已全部处理完毕：

1
all_data.isnull().sum().max()

0

进一步挖掘特征

我们注意到有些特征虽然是数值型的，但其实表征的只是不同类别，其数值的大小并没有实际意义，因此我们将其转化为类别特征。

1
2
3
all_data['MSSubClass'] = all_data['MSSubClass'].astype(str)
all_data['YrSold'] = all_data['YrSold'].astype(str)
all_data['MoSold'] = all_data['MoSold'].astype(str)

反过来，有些类别特征实际上有高低好坏之分，这些特征的质量越高，就可能在一定程度导致房价越高。我们将这些特征的类别映射成有大小的数字，以此来表征这种潜在的偏序关系。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
all_data['FireplaceQu'] = all_data['FireplaceQu'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['GarageQual'] = all_data['GarageQual'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['GarageCond'] = all_data['GarageCond'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['GarageFinish'] = all_data['GarageFinish'].map({'Fin': 3, 'RFn': 2, 'Unf': 1, 'None': 0})
all_data['BsmtQual'] = all_data['BsmtQual'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['BsmtCond'] = all_data['BsmtCond'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['BsmtExposure'] = all_data['BsmtExposure'].map({'Gd': 4, 'Av': 3, 'Mn': 2, 'No': 1, 'None': 0})
all_data['BsmtFinType1'] = all_data['BsmtFinType1'].map({'GLQ': 6, 'ALQ': 5, 'BLQ': 4, 'Rec': 3, 'LwQ': 2, 'Unf': 1, 'None': 0})
all_data['BsmtFinType2'] = all_data['BsmtFinType2'].map({'GLQ': 6, 'ALQ': 5, 'BLQ': 4, 'Rec': 3, 'LwQ': 2, 'Unf': 1, 'None': 0})
all_data['ExterQual'] = all_data['ExterQual'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['ExterCond'] = all_data['ExterCond'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['HeatingQC'] = all_data['HeatingQC'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['PoolQC'] = all_data['PoolQC'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['KitchenQual'] = all_data['KitchenQual'].map({'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0})
all_data['Functional'] = all_data['Functional'].map({'Typ': 8, 'Min1': 7, 'Min2': 6, 'Mod': 5, 'Maj1': 4, 'Maj2': 3, 'Sev': 2, 'Sal': 1, 'None': 0})
all_data['Fence'] = all_data['Fence'].map({'GdPrv': 4, 'MnPrv': 3, 'GdWo': 2, 'MnWw': 1, 'None': 0})
all_data['LandSlope'] = all_data['LandSlope'].map({'Gtl': 3, 'Mod': 2, 'Sev': 1, 'None': 0})
all_data['LotShape'] = all_data['LotShape'].map({'Reg': 4, 'IR1': 3, 'IR2': 2, 'IR3': 1, 'None': 0})
all_data['PavedDrive'] = all_data['PavedDrive'].map({'Y': 3, 'P': 2, 'N': 1, 'None': 0})
all_data['Street'] = all_data['Street'].map({'Pave': 2, 'Grvl': 1, 'None': 0})
all_data['Alley'] = all_data['Alley'].map({'Pave': 2, 'Grvl': 1, 'None': 0})
all_data['CentralAir'] = all_data['CentralAir'].map({'Y': 1, 'N': 0})

利用一些重要的特征构造更多的特征：

1
2
3
4
5
all_data['TotalSF'] = all_data['TotalBsmtSF'] + all_data['1stFlrSF'] + all_data['2ndFlrSF']
all_data['OverallQual_TotalSF'] = all_data['OverallQual'] * all_data['TotalSF']
all_data['OverallQual_GrLivArea'] = all_data['OverallQual'] * all_data['GrLivArea']
all_data['OverallQual_TotRmsAbvGrd'] = all_data['OverallQual'] * all_data['TotRmsAbvGrd']
all_data['GarageArea_YearBuilt'] = all_data['GarageArea'] + all_data['YearBuilt']

Box-Cox变换

对于数值型特征，我们希望它们尽量服从正态分布，也就是不希望这些特征出现正负偏态。

那么我们先来计算一下各个特征的偏度：

1
2
3
4
5
6
numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index

# Check the skew of all numerical features
skewed_feats = all_data[numeric_feats].apply(lambda x: skew(x.dropna())).sort_values(ascending=False)
skewness = pd.DataFrame({'Skew': skewed_feats})
skewness.head(10)
Skew
MiscVal 21.940
PoolQC 19.549
PoolArea 17.689
LotArea 13.109
LowQualFinSF 12.085
3SsnPorch 11.372
KitchenAbvGr 4.301
BsmtFinSF2 4.145
Alley 4.137
EnclosedPorch 4.002

可以看到这些特征的偏度较高，需要做适当的处理。这里我们对数值型特征做Box-Cox变换，以改善数据的正态性、对称性和方差相等性。更多关于Box-Cox变换的知识可以参考这篇博客：https://blog.csdn.net/sinat_26917383/article/details/77864582

1
2
3
4
5
6
7
8
skewness = skewness[abs(skewness['Skew']) > 0.75]
print("There are {} skewed numerical features to Box Cox transform".format(skewness.shape[0]))

from scipy.special import boxcox1p
skewed_features = skewness.index
lam = 0.15
for feat in skewed_features:
    all_data[feat] = boxcox1p(all_data[feat], lam)

There are 41 skewed numerical features to Box Cox transform

独热编码

对于类别特征，我们将其转化为独热编码，这样既解决了模型不好处理属性数据的问题，在一定程度上也起到了扩充特征的作用。

1
2
all_data = pd.get_dummies(all_data)
print(all_data.shape)

(2917, 254)

现在我们有了经过处理后的训练集和测试集：

1
2
train = all_data[:ntrain]
test = all_data[ntrain:]

至此，特征工程就算完成了。

建立模型

导入算法包：

1
2
3
4
5
6
7
8
9
from sklearn.linear_model import ElasticNet, Lasso
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.kernel_ridge import KernelRidge
from sklearn.preprocessing import RobustScaler
from sklearn.base import BaseEstimator, TransformerMixin, RegressorMixin, clone
from sklearn.model_selection import KFold, cross_val_score
from sklearn.metrics import mean_squared_error
import xgboost as xgb
import lightgbm as lgb

标准化

由于数据集中依然存在一定的离群点，我们首先用RobustScaler对数据进行标准化处理。

1
2
3
scaler = RobustScaler()
train = scaler.fit_transform(train)
test = scaler.transform(test)

评价函数

先定义一个评价函数。我们采用5折交叉验证。与比赛的评价标准一致，我们用Root-Mean-Squared-Error (RMSE)来为每个模型打分。

1
2
3
4
5
6
7
#Validation function
n_folds = 5

def rmsle_cv(model):
    kf = KFold(n_folds, shuffle=True, random_state=42).get_n_splits(train.values)
    rmse= np.sqrt(-cross_val_score(model, train.values, y_train, scoring="neg_mean_squared_error", cv = kf))
    return(rmse)

基本模型

  • 套索回归
1
lasso = Lasso(alpha=0.0005, random_state=1)
  • 弹性网络
1
ENet = ElasticNet(alpha=0.0005, l1_ratio=.9, random_state=3)
  • 核岭回归
1
KRR = KernelRidge(alpha=0.6, kernel='polynomial', degree=2, coef0=2.5)
  • 梯度提升回归
1
2
3
4
GBoost = GradientBoostingRegressor(n_estimators=1000, learning_rate=0.05,
                                   max_depth=4, max_features='sqrt',
                                   min_samples_leaf=15, min_samples_split=10, 
                                   loss='huber', random_state =5)
  • XGBoost
1
2
3
4
5
6
model_xgb = xgb.XGBRegressor(colsample_bytree=0.5, gamma=0.05, 
                             learning_rate=0.05, max_depth=3, 
                             min_child_weight=1.8, n_estimators=1000,
                             reg_alpha=0.5, reg_lambda=0.8,
                             subsample=0.5, silent=1,
                             random_state =7, nthread = -1)
  • LightGBM
1
2
3
4
5
6
model_lgb = lgb.LGBMRegressor(objective='regression',num_leaves=5,
                              learning_rate=0.05, n_estimators=1000,
                              max_bin = 55, bagging_fraction = 0.8,
                              bagging_freq = 5, feature_fraction = 0.2,
                              feature_fraction_seed=9, bagging_seed=9,
                              min_data_in_leaf =6, min_sum_hessian_in_leaf = 11)

看看它们的表现如何：

1
2
3
4
5
6
7
8
9
10
11
12
score = rmsle_cv(lasso)
print("\nLasso score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(ENet)
print("ElasticNet score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(KRR)
print("Kernel Ridge score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(GBoost)
print("Gradient Boosting score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(model_xgb)
print("Xgboost score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
score = rmsle_cv(model_lgb)
print("LGBM score: {:.4f} ({:.4f})\n" .format(score.mean(), score.std()))

Lasso score: 0.1115 (0.0073)

ElasticNet score: 0.1115 (0.0073)

Kernel Ridge score: 0.1189 (0.0045)

Gradient Boosting score: 0.1140 (0.0085)

Xgboost score: 0.1185 (0.0081)

LGBM score: 0.1175 (0.0079)

Stacking方法

集成学习往往能进一步提高模型的准确性，Stacking是其中一种效果颇好的方法，简单来说就是学习各个基本模型的预测值来预测最终的结果。详细步骤可参考：https://www.jianshu.com/p/59313f43916f

这里我们用ENet、KRR和GBoost作为第一层学习器，用Lasso作为第二层学习器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class StackingAveragedModels(BaseEstimator, RegressorMixin, TransformerMixin):
    def __init__(self, base_models, meta_model, n_folds=5):
        self.base_models = base_models
        self.meta_model = meta_model
        self.n_folds = n_folds
   
    # We again fit the data on clones of the original models
    def fit(self, X, y):
        self.base_models_ = [list() for x in self.base_models]
        self.meta_model_ = clone(self.meta_model)
        kfold = KFold(n_splits=self.n_folds, shuffle=True, random_state=156)
        
        # Train cloned base models then create out-of-fold predictions
        # that are needed to train the cloned meta-model
        out_of_fold_predictions = np.zeros((X.shape[0], len(self.base_models)))
        for i, model in enumerate(self.base_models):
            for train_index, holdout_index in kfold.split(X, y):
                instance = clone(model)
                self.base_models_[i].append(instance)
                instance.fit(X[train_index], y[train_index])
                y_pred = instance.predict(X[holdout_index])
                out_of_fold_predictions[holdout_index, i] = y_pred
                
        # Now train the cloned  meta-model using the out-of-fold predictions as new feature
        self.meta_model_.fit(out_of_fold_predictions, y)
        return self
   
    #Do the predictions of all base models on the test data and use the averaged predictions as 
    #meta-features for the final prediction which is done by the meta-model
    def predict(self, X):
        meta_features = np.column_stack([
            np.column_stack([model.predict(X) for model in base_models]).mean(axis=1)
            for base_models in self.base_models_ ])
        return self.meta_model_.predict(meta_features)

Stacking的交叉验证评分：

1
2
3
4
stacked_averaged_models = StackingAveragedModels(base_models = (ENet, GBoost, KRR),
                                                 meta_model = lasso)
score = rmsle_cv(stacked_averaged_models)
print("Stacking Averaged models score: {:.4f} ({:.4f})".format(score.mean(), score.std()))

Stacking Averaged models score: 0.1081 (0.0085)

我们得到了比单个基学习器更好的分数。

建立最终模型

我们将XGBoost、LightGBM和StackedRegressor以加权平均的方式融合在一起，建立最终的预测模型。

先定义一个评价函数：

1
2
def rmsle(y, y_pred):
    return np.sqrt(mean_squared_error(y, y_pred))

用整个训练集训练模型，预测测试集的房价，并给出模型在训练集上的评分。

  • StackedRegressor
1
2
3
4
stacked_averaged_models.fit(train, y_train)
stacked_train_pred = stacked_averaged_models.predict(train)
stacked_pred = np.expm1(stacked_averaged_models.predict(test))
print(rmsle(y_train, stacked_train_pred))

0.08464515778854238

  • XGBoost
1
2
3
4
model_xgb.fit(train, y_train)
xgb_train_pred = model_xgb.predict(train)
xgb_pred = np.expm1(model_xgb.predict(test))
print(rmsle(y_train, xgb_train_pred))

0.08362948457258125

  • LightGBM
1
2
3
4
model_lgb.fit(train, y_train)
lgb_train_pred = model_lgb.predict(train)
lgb_pred = np.expm1(model_lgb.predict(test))
print(rmsle(y_train, lgb_train_pred))

0.06344397467222622

融合模型的评分：

1
2
print('RMSLE score on train data:')
print(rmsle(y_train,stacked_train_pred*0.70 + xgb_train_pred*0.15 + lgb_train_pred*0.15))

RMSLE score on train data: 0.07939492590501797

预测

1
ensemble = stacked_pred*0.70 + xgb_pred*0.15 + lgb_pred*0.15

生成提交文件

1
2
3
4
sub = pd.DataFrame()
sub['Id'] = test_ID
sub['SalePrice'] = ensemble
sub.to_csv('submission.csv', index=False)